Description

Given a linked list, return the node where the cycle begins. If there is no cycle, return null.

To represent a cycle in the given linked list, we use an integer pos which represents the position (0-indexed) in the linked list where tail connects to. If pos is -1, then there is no cycle in the linked list.

Note: Do not modify the linked list.

Example

Example 1

1
2
3
4
Input: head = [3,2,0,-4], pos = 1
Output: tail connects to node index 1
Explanation: There is a cycle in the linked list, where tail connects to the
second node.

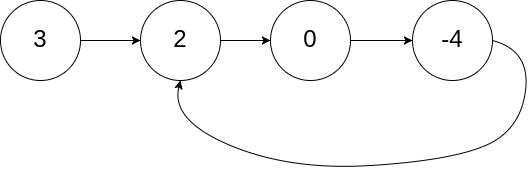
Example 2

1
2
3
4
Input: head = [1,2], pos = 0
Output: tail connects to node index 0
Explanation: There is a cycle in the linked list, where tail connects to the
first node.

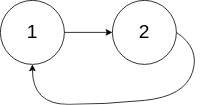
Example 3

1
2
3
Input: head = [1], pos = -1
Output: no cycle
Explanation: There is no cycle in the linked list.

Interface

1
2
3
4
5
6
7
8
9
10
11
12
13
14
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        
    }
};

Solution

使用 stl::map

map<ListNode*, int> 将 ListNode* 与 ListNode* 出现的次数进行对应，如果单链表中不存在环则，则遍历到尾结点的 next 指向的 nullptr 时就会结束遍历，返回 nullptr；而如果单链表中存在环，第一个出现次数大于 1 的结点即环的入口结点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        if (head == nullptr) return nullptr;
        map<ListNode*, int> lmap;
      	ListNode *node = head;
        while (node != nullptr) {
            if (lmap.count(node) > 0) break;
            else (lmap[node] = 1);
            node = node->next;
        }
        return node;
    }
};

使用 stl::set

与使用 stl::map 的思路相似，故不再叙述。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        if (head == nullptr) return nullptr;
        set<ListNode*> nodeset;
        while (head != nullptr) {
            if (nodeset.count(head) > 0) return head;
            nodeset.insert(head);
            head = head->next;
        }
        return nullptr;
    }
};

Improvement

使用快慢指针

设定两个指针，一个慢指针，一个快指针，慢指针一次走的距离是一个结点，而快指针一次走的距离是两个结点，即快指针的速度是慢指针的两倍。

此时，会出现两种情况：

  • 单链表中不存在环则：快指针往后遍历的过程中，会遍历到 nullptr 结点，即单链表中不存在环，最后一个结点指向的是 nullptr。

  • 单链表中存在环则：由于存在环，则快慢指针最后都会进入环中并在环中一直循环，由于快慢指针存在速度差，只要快慢指针一直在环中循环，最终会在环中的一个结点相遇，相遇时快指针至少在环中循环了一圈。

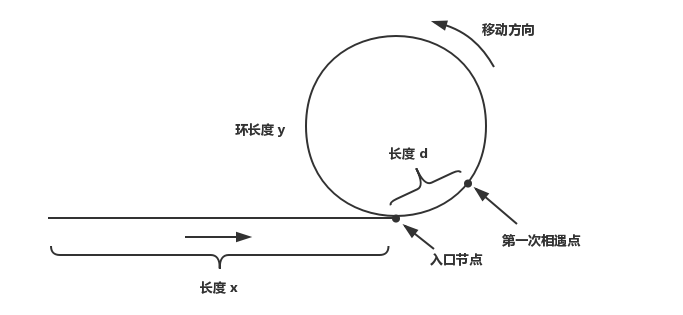
    • 如果这时快指针已经是在环里走了 1 圈（对应于非环部分较短的情况）：

      此时快指针走了 2(x + d) (0 <= d) 距离，2(x + d) = x + y + d ，可得 x = y - d ，此时再同时从第一次相遇点和头结点出发，速度都为一个结点每次，最后两指针会在环入口结点处相遇。

    • 如果这时快指针已经是在环里走了不止一圈，假设为 k 圈：

      此时快指针走了 2(x + d) (0 <= d)​ 距离，2(x + d) = x +ky + d​，可得 x = ky - d​ ，此时再同时从第一次相遇点和头结点出发，速度都为一个结点每次，最后两指针也会在环入口结点处相遇。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        if (head == nullptr) return nullptr;
      	ListNode *slow = head, *fast = head;
      	do {
            if (fast->next != nullptr && fast->next->next != nullptr) {
                slow = slow->next;
                fast = fast->next->next;
            } else {
                return nullptr;
            }
      	} while (slow != fast);
      	fast = head;
        while (slow != fast) {
            slow = slow->next;
            fast = fast->next;
        }
        return fast;
    }
};

详细思路参考：一个链表中包含环，请找出该链表的环的入口结点